Attention is all you need (Draft)

Transformers are based solely & completely on attention mechanism.

Transformers completely removed recurrence and convolutions to make computation parallelizable i.e. faster training times but more importantly, capturing long-range dependencies.

Mathematical Proof:

Q. Follow-up: How Transformer solves this?

Ans: One key factor affecting the ability to learn long-term dependencies is the length of the paths forward and backward signals have to traverse in the network. The shorter these paths between any combination of positions in the input and output sequences, the easier it is to learn long-range dependencies.

A self-attention layer connects all positions with a constant number of sequentially executed operations, whereas

a recurrent layer requires O(n) sequential operations, and

a single convolutional layer with kernel width k < n does not connect all pairs of input and output positions. Doing so requires a stack of O(n/k) convolutional layers in the case of contiguous kernels.

Q. Follow-up: Why Recurrent Models are slow?

Ans: Recurrent Models generate a sequence of hidden states \(h_t\), as a function of the previous hidden state \(h_{t−1}\) and the input for position t. This inherently sequential nature (1) precludes parallelization within training examples, and (2) for longer sequence lengths you start to encounter memory constraints. So, in such cases you need to truncate the size of the sequences.

Q. Follow-up: Why convolution is slow?

Ans: In Convolution number of operations required to relate signals from two arbitrary input or output positions grows with distance between the position- this makes it more difficult to learn dependencies between distant positions. (Hint: O(n/k)). Transformers reduce this to a constant number of oprations.

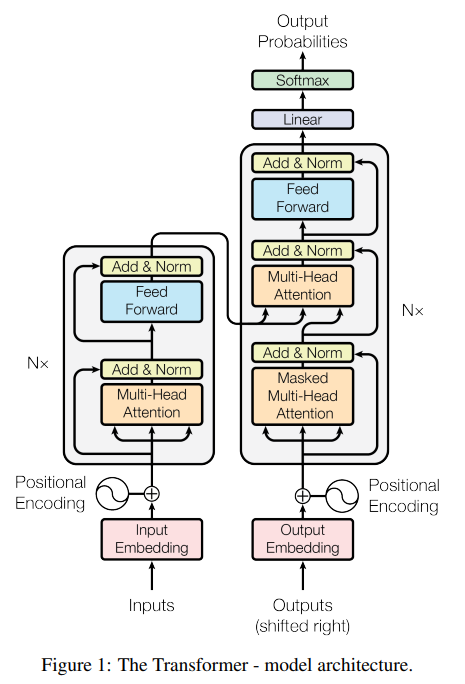
Transformer Architecture

Encoder Decoder Architecture - where architecture uses stacked self-attention and point-wise, fully connected layers for both the encoder and decoder

Encoder Stack

• Stack of 6 identical layers
• Each layer has 2 sub-layers
• First sub-layer: MSA (Multi-headed self-attention)
• Second sub-layer: Point-wise Fully-Connected Feed Forward Network
• Also, there is a Residual connection and LayerNorm across each sublayer (i.e. output of each sub-layer is LayerNorm(x + Sublayer(x)))

Decoder Stack

• Stack of 6 identical layers
• Each layer has 3 sub-layers
• First sub-layer: MSA (Masked Multi-headed self-attention)
• Second sub-layer: MA (Multi-headed attention over the output of the encoder stack) : CROSS-ATTENTION
• Third sub-layer: Point-wise Fully-Connected Feed Forward Network
• Also, there is a Residual connection and LayerNorm across each sublayer (i.e. output of each sub-layer is LayerNorm(x + Sublayer(x)))

Attention

“An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.”

“The output is computed as a weighted sum of the values…” - means softmax(…)*V

“…where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.” - means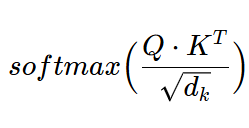

Q. What is Attention Mechanism?

Ans: ??

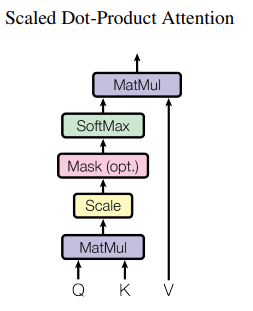
Scaled Dot-Product Attention

They called the attention “Scaled Dot-Product Attention” because it involves scaling with square root of dimension \(\sqrt{d_k}\) + they scale the output with Softmax and the calculation involves dot product between Q & K.

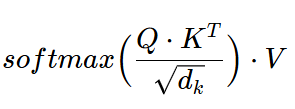
Q: What is Dot-Product Attention vs Scaled Dot-Product Attention?

Ans:Dot-Product Attention is commonly called multiplicative attention. It is identical to Scaled Dot-product attention explained above except that it does not peform scaling with \(\sqrt{d_k}\). In such cases, what happens is that for large dimension \(d_k\) values, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, they scaled the dot products by \(1/\sqrt{d_k}\)

Q: What is additive attention? Prior research suggests it works better than multiplicative attention. The why authors did not use it?

Ans: Additive attention computes the compatibility function using a feed-forward network witha single hidden layer. While the Additive and Multiplicative are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.

Also, note that it works better than multiplicative attention (vanilla w/o scaling) for large dimension \(d_k\) values only because of the probable small gradients in vanilla multiplicative attention (as explained in para above). Whereas for small \(d_k\) values, both additive and dot-product are equally well.

Now, having said that researchers found that using scaling, the multiplicative attention could be significantly improved for large \(d_k\).

Self-attention (intra-attention)

Self-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.

Multi-Head Attention

Instead of performing a single attention function with \(d_model\) -dimensional keys, values and queries, they found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to \(d_k\), \(d_k\) and \(d_v\) dimensions, respectively. Attention from each head is computed, concatenated and once again projected, resulting in the final value as shown below:

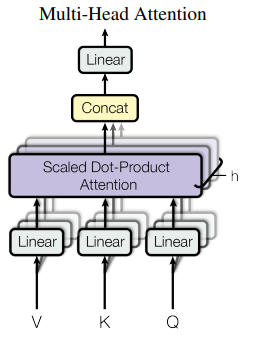
Q: Why multi-head why not single-head?

Ans:

Computational wise it is same + you learn more

Excerpts

“relying entirely on an attention mechanism to draw global dependencies between input and output”

(Mine) - RNNs: global dependencies is constraint in RNNs + processing is sequential (not parallelizable).

Convolutions: Allows some parallelization. But number of operations required to capture global relations b/w 2 input positions grows exponentially - thus again difficult to capture long-term (global) dependencies